नमस्कार दोस्तों , आज हम Geometry के बारे में कुछ basic concept को समझने का प्रयास करेंगे , Geometry का इतिहास बहुत पुराना है ,Geometry को हिंदी में ज्यामिति कहा जाता है यह यूनानी शब्द geometron से मिलकर बना है जिसका मतलब होता है भूमि मापन. अर्थात पहले के ज़माने में लोग Geometry का का प्रयोग भूमि को मापने में किया करते थे.

Geometry के Basic Concept को समझने का प्रयास करिए

दोस्तों Geometry को बुनियादी तौर पर समझने के लिए first of all इसके कुछ basic concept को समझना बहुत ही जरुरी है तो चलिए Geometry के Basic Concept को इनके परिभाषा से समझने का प्रयास करते है.

बिंदु (Point):-

बिंदु एक ऐसा ज्यामितीय (Geometrical) रचना है जिसमे नहीं लम्बाई होती है ,नहीं चौड़ाई होती है नहीं ऊंचाई होती है नहीं मोटाई होती केवल एक स्थान अथवा स्थिति मात्र होती है बिंदु कहलाती है जैसे –

ऊपर A और B दो बिन्दुओ के उदहारण है.

हमारे दैनिक जीवन में pencil का नोक अथवा pen का नोक बिंदु (point) का उदहारण है

Note -> दुसरे शब्दों में हम कह सकते है की- एक एसा वृत जिसका त्रिज्या 0 होती है बिंदु (point) कहलाती है.

रेखाखण्ड (Line Segment) :-

दो बिन्दुओ को मिलाने वाली सीधी ज्यामितीय पथ को रेखाखण्ड कहा जाता है इसके दो अंत बिंदु होते है

उदहारण के लिए मान लिए जाय की A और B दो अंत बिंदु है इसको एक धागे से इसप्रकार बांध दिए जाये की धागा ढीला न रहे तो इसे रेखाखंड(Line Sigment) कहा जायेगा. इसे निचे दिए गए चित्र से समझने का प्रयास करते है.

ऊपर दिए गए दोनों रेखाए रेखाखण्ड के उदहारण है यहाँ पर AB और CD रेखा खंड के उदहारण है इसको हम AB¯ और CD‾ के द्वारा अर्थात AB और CD के ऊपर (–) का चिन्ह दे कर दर्शाते है यहाँ पर A और B रेखाखण्ड AB का अंत बिंदु है और C और D रेखाखण्ड CD के अंत बिंदु है. रेखाखंड AB को हम BA और CD को DC भी लिख सकते है.

रेखा (Line) :-

यदि किसी रेखाखण्ड के दोनों सिरों को दोनों ओर इसके इसके दोनों तरफ इसके बिपरीत दिशाओ में बिना किसी अंत के बढ़ा दिया जाय तो हमें रेखा प्राप्त होती है

यदि कोई रेखाखण्ड AB है और दूसरा रेखाखंड CD है और दोनों रेखाखंडो के दोनों सिरों A,B और C,D को दोनों तरफ बढ़ा दिया जाय तो जो हमें मिलाता है वह रेखा होगा जैसा की निचे दिए गए चित्र में दिखाया गया है-

रेखा को किसी single letter से भी दर्शाया जाता है जैसे की AB को L से दिखाया गया है और CD को M द्वारा दिखाया गया है.संकेत के लिए हम AB और CD के उपर (<–>) लगाकर दिखाते है

प्रतिछेदी रेखाएं (Intersecting lines):-

जब दो रेखाएं आपस में किसी बिंदु पर पतिछेदित करती है तो दोनों रेखाएं प्रतिछेदी रेखाएं कहलाती है और दोनों रेखाए जिस बिंदु पर प्रतिछेदित करती है उस विन्दु को प्रतिछेदी विन्दु कहते है. जैसे –

जैसा की ऊपर चित्र में दिखाया गया है की L और M दो परतिछेदि रेखाएं है जो कि परतिछेदि विनदु p पर एक दुसरे को परतिछेदित करति हैं.

दो रेखायें एक से अधिक विन्दु पर परतिछेदित नहि कर सकति है .
दो से अधिक रेखाएं एक विन्दु पर परतिछेदित कर सकति है .

समान्तर रेखाएं (Parallel lines ) :-

वैसी रेखाएं जिनके दोनों सिरों को जितना भी आगे बढाया जाय वो आपस में प्रतिछेदित नहीं करति है समान्तर रेखाए (parallel lines ) कहलाती है.जैसे-

जैसा की ऊपर चित्र में दिखाया गया है AB और CD दोनों समान्तर रेखाये है

यदि दोनों रेखाओ के दोनों सिरों को कितना भी आगे की ओर बढाया जाय ये आपस में एक दुसरे को कभी भी प्रतिछेदित नहीं करेंगी .

यदि दो रेखाएं AB और CD दो समान्तर रेखांये है तो इसे हम संकेत के रूप में AB||CD लिखेंगे.

किरण (Ray):-

किरण रेखा का एक एसा भाग होता है जो किसी एक बिंदु से प्रारंभ होती है और एक ही दिसा में बिना कीसी अंत के बढती जाती है, और जिस बिंदु से यह प्रारंभ होती है इसे हम प्रारंभिक बिंदु कहते है. जैसे –

जैसा की ऊपर चित्र में दिखाया गया है की AP एक किरण है यह विन्दु A से सुरु होता है और एक ही दिशा में बढ़ती जाती है

यहाँ पर A प्रारंभिक बिंदु है और इस किरण पर p एक बिंदु है .

किरण को AB के ऊपर (–>) लिख कर दिखाया जाता है.

हमारे दैनिक जिवंन में सूर्य के प्रकास को किरण का उदाहरण है क्योंकी सूर्य का प्रकास सूर्य से निकलती है और एक ही दिसा में बढती जाती है यहाँ पर प्रारंभिक बिंदु सूर्य होगा .

ठीक इसी प्रकार हमारे घरों में उपयोग होने वाले टार्च से निकालने वाले प्रकास भी किरण के उदहारण है .

दोस्तों हम Geometry में सरल रेखाओं से बनी आकृतियों के बारे में आगे जानेंगें.

वक्र (Curve) :-

टेढ़ी – मेढ़ी रेखाओं से जो भी आकृतियाँ हमें प्राप्त होता है वक्र (Curve) कहलाता है. दोस्तों वक्र के दो प्रकार होते है जो की निचे दिया गया है

खुला वक्र (Open Curve)
बंद वक्र (Closed Curve)

अब हम दोनों प्रकारों के वक्रो को इनके परिभासा के साथ समझने का प्रयास करेंगे

(1)खुला वक्र (Open Curve) :-

वैसे वक्र जिनकी रेखाये आपस में नहीं मिलती है या नहीं काटती खुला वक्र कहलाता है अथवा वैसे वक्र जो खुला हुआ हो खुला वक्र कहलाता है.

जैसा की ऊपर दिखाया गया है Geometry-fig a और Geometry-fig b दोनों ही खुले वक्र (open curve) के उदहारण है.

(2)बंद वक्र (Closed Curve) :-

वैसे वक्र जिनकी रेखाएं आपस में काटती है या एक जगह आकार मिलती है बंद वक्र (Closed Curve ) कहलाती है. बंद वक्र बाहर से बंद होती है जैसे –

जैसा की ऊपर fig-a और fig-b में दिखाया गया है दोनों fig closed curve के उदाहरण है ,बंद वक्र के तिन भाग होते है –

(1)वक्र के अभ्यंतर (interior of curve)- वक्र के अन्दर का भाग

(2)वक्र के परिसीमा (boundary of curve) -वक्र पर

(3)वक्र का वहिर्भाग (exterior of curve)- वक्र का बाहर का भाग

बहुभुज(Polygons) :-

रेखाखंडों से बनी सरल बंद आकृति को हम बहुभुज (Polygons) कहते है.

और किसी बहुभुज को बनाने वाली रेखाखंड को हम भुजाये या किनारा (sides) कहते है. जैसा की निचे दिखाया गया है-

बहुभुज की भुजाएं (Sides of Polygons) :-

बहुभुज को बनाने वाली रेखाखंड को बहुभुज की भुजाएं(sides) कहा जाता है. किसि भी बहुभुज में जीतनी भुजाएं होती है वह बहु भुज उतने भुजाओ वाली वहुभुज कहलाती है.

जैसा की उपर fig में दिखाया गया है इस fig में टोटल 5 भुजाएं है इसलिए इसको पंचभुज कहा जायेगा.

ऊपर दिए गए पंचभुज में पांच भुजाएं AB, BC ,CD , DE , EA है.

बहुभुज की शीर्ष (Vertex of Polygons) :-

किसी बहुभुज में बहुभुज की दो भुजाएं जिस बिंदु पर मिलती है वह विन्दु उस बहुभुज(Polygons) का शीर्ष(vertex) कहलाता है.

जैसा की ऊपर fig में दिखाया गया है- भुजा AB और BC शीर्ष B पर मिलते है इसलिए B दिए गए बहुभुज का शीर्ष कहलायेगा.

दिए गए बहुभुज ABCDE में A ,B C , D और E दिए गए बहुभुज के शीर्ष है.

बहुभुज की आसन्न भुजाएं (Adjacent Sides of Polygon):-

किसी भी बहुभुज की वैसी दो भुजाये जिसकी एक उभयानिस्ट अंत बिंदु(common end point ) हो बहुभुज की आसन्न भुजाये(Adjacent Sides) कहलाता है.

जैसा की ऊपर fig में दिखाया गया है- AB और BC किसी दिए गए बहुभुज की आसन्न भुजाएं(Adjacent Sides)है

इसमे दोनों भुजाओं AB और BC में शीर्ष(vertex) B एक उभयानिस्ट अंत बिंदु है.

AEऔरDC बहुभुज के आसन्न भुजाये नहीं है क्यों की इन दोनों भुजाओं में कोई भी बिंदु उभयानिस्ट नहीं है.

बहुभुज के आसन्न शीर्ष(Adjacent Vertex):-

किसी बहुभुज में किसी एक ही भुजा के अंत बिंदु को बहुभुज के आसन्न शीर्ष (Adjacent Vertex) कहलाते है.

ऊपर दिए गए बहूभुज में भुजा AB का adjacent शीर्ष AऔरB है.ठीक इसी प्रकार CD के आसन्न शीर्ष CऔरD है.

लेकिन A और C दोनो आसन्न शीर्ष नहीं है क्यों की दोनों शीर्ष एक ही भुजा के शीर्ष नहीं है.

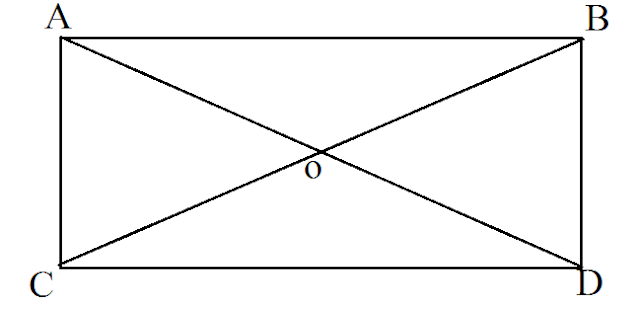
बहुभुज का विकर्ण (Diagonals of Polygons) :-

किसी बहुभुज की अभ्यंतर (भीतर ) दो भुजाओं को मिलाने वाली रेखा को हम बहुभुज का विकर्ण(Diagonals) कहते है.

किसी बहुभुज में वैसे शीर्ष जो आसन्न शीर्ष नहीं है को मिलाने से हमें बहुभुज का विकर्ण प्राप्त होता है.

ऊपर दिए गये बहुभुज में AC ,AD , EB , EC ,BE और BD बहुभुज में विकर्ण है .

दोस्तों Geometry में यदि सरल रेखाओं से मिलकर यदि कोई भी एक बंद आकृति वनती है तो वह एक प्रकार का बहुभुज ही होगा.

कोण (Angle) :-

दो किरणों को किसी एक उभयनिस्ट बिंदु पर मिलने से जो झुकाव प्राप्त होता है उसे कोण कहा जाता है.

अथवा दुसरे शब्दों में कहेंगे की-

कोण वह झुकाव है जो दो किरणों को एक उभयनिस्ट बिंदु पर मिलने हमें कोने(Corner) के रूप में प्राप्त होता है .

जैसा की निचे fig में दिखाया गया है .

ऊपर दिए गए fig में ABC कोण का उदहारण है कोण को (∠) द्वारा दिखाया जाता है.

दिए गए कोण को ∠ABC लिखेगें इसको इसके बिच की alphabets से भी दिखाया जा सकता है जैसे ∠B .

कोण बनाने के बाद चाप को दिखाना बहुत जरुरी होता है.

ऊपर दिए गए कोण में AB और BC दो किरणे है इसको भुजाये (sides) भी बोला जा सकता है.और B दोनों किरणों का प्रारंभिक बिंदु है.

कोण हमेसा दो किरणों को मिलाने वाली उभयनिस्ट विन्दु पर ही बनता है.यह कोण का शीर्ष (vertex) कहलाता है. B इस कोण का शीर्ष बिदु (vertex) है.

कोण ∠ABC को कोण ∠CBA भी लिख सकते है.

त्रिभुज (Triangle) :-

तिन रेखाओं अथवा भुजाओं (sides) से घिरे हुए क्षेत्र को रिभुज (Triangle) कहा जाता है .

दुसरे शब्दों में कहेंगे की वैसे बहुभुज जिसमें तिन भुजाएं है त्रिभुज कहाजाता है.त्रिभुज सबसे कम भुजाओं वाली बहुभुज है.

जैसा की निचे fig में दिखाया गया है

जैसा की ऊपर fig में दिखाया गया है – त्रिभुज को “Δ ” symbol द्वारा दिखाया जाता है ऊपर दिए गए त्रिभुज को हम ΔABC भी लिख सकते है.

AB , BC और CA त्रिभुज की भुजाये (Sides) है . और ∠ABC ,∠CAB और∠ACB त्रिभुज के तिन कोंण है इसको ∠B ,∠A और∠C भी लिख सकते है .

एवं A ,B , और C त्रिभुज की शीर्ष (vertex) है.

चतुर्भुज (Quadrilateral) :-

चार भुजाओं से घिरे हुए क्षेत्र को चतुर्भुज कहा जाता है.चतुर्भुज एक चार भुजाओ वाला बहुभुज है.

जैसा की निचे fig में दिखाया गया है-

ऊपर दिए गए fig में ABCD एक चतुर्भुज है , AB ,BC ,CD ,DA इस चतुर्भुज की चार भुजाए है.और ∠A , ∠B , ∠C और ∠D इसके चार कोण है. और A ,B ,C ,D इसके चार शीर्ष(vertex ) हैं. चतुर्भुज में AB और AC दो आसन्न भुजाएं है. ठीक इसीप्रकार BD और DC भी दो आसन्न भुजाये है.

चतुर्भुज की आसन्न भुजाएं (Adjacent Sides of Quadrilateral):-

चतुर्भुज ABCD में AB और AC दो आसन्न भुजाएं है.

ठीक इसीप्रकार BD और DC भी दो आसन्न भुजाये है.

चतुर्भुज की सम्मुख भुजाएं ( Opposite Sides of Quadrilateral):-

चतुर्भुज ABCD में AB और CD दो सम्मुख भुजाएं (Opposite Sides) है .

ठीक इसीप्रकार AC और BD भी सम्मुख भुजाये है.

चतुर्भुज की आसन्न कोण (Adjacent Angle of Quadrilateral):-

चतुर्भुज ABCD में कोण ∠A और कोण ∠B दो आसन्न कोण (Opposite Angle)है.

ठीक इसीप्रकार कोण ∠C और कोण ∠D भी दो आसन्न कोण है.

चतुर्भुज की सम्मुख कोण (Opposite Angle of Quadrilateral):-

चतुर्भुज ABCD में कोण ∠B और कोण ∠D दो सम्मुख कोण (Opposite Angle) है ,ठीक इसीप्रकार कोण ∠A और कोण ∠C भी सम्मुख कोण है.

वृत (Circle) :-

किसी विन्दु से किसी निश्चित रेखा के बराबर किसी वस्तु को घुमाने पर जो पथ का निर्माण होता है उसे वृत कहा जाता है

जैसे पहिया , चूड़ी , सिक्का इत्यादि वृत का उदहारण है

दुसरे शब्दों में-

वैसा विन्दु पथ जिसके किसी विन्दु से किसी निश्चित विन्दु का दुरी बराबर होता है वह विन्दु पथ वृत कहलाता है.

Note :- दोस्तों वृत का यह परिभासा आपको समझ में न आये यह आपको higher classes में पढ़ने को मिलेगा.

अब हम वृत को निचे दिए गए fig के साथ समझने का प्रयास करेंगे.

जैसा की ऊपर दिए गए fig में दिखाया गया है AOB एक वृत(circle) है.

वृत की त्रिज्या (Radius of Circle) :-

किसी वृत में केंद्र से परिधि के किसी विन्दु को मिलाने वाली रेखा को वृत की त्रिज्या कहा जाता है.

मान लिया की A वृत के परिधी पर कोई विन्दु है और O वृत का केंद्र है , तो इए गए fig में O को A से मिलाने वाली रेखा OA वृत की त्रिज्या है.

किसी वृत में बराबर माप के अनेक त्रिज्याए हो सकति है दुसरे शब्दों में –

वृत परिधि के किसी विन्दु से वृत के केंद्र से मिलाने वाली रेखा को वृत की त्रिज्या कहा जाता है.

वृत की त्रिज्या को हम r या R द्वारा दिखाते है.

ऊपर दिए गए fig में OA ,OB,OC ,OD वृत की त्रिज्याएँ है तो – OA = OB = OC = OD होगा

वृत की केंद्र (Center of Circle ) :-

वृत की दो त्रिज्याए जिस विन्दु पर आकार मिलता है वह विन्दु वृत का केंद्र कहलाता है.

दिए गए fig में O वृत का केंद्र है , वृत की त्रिज्याएँ OA ,OB,OC ,OD विन्दु O पर आकर मिलती है.

वृत का केंद्र वृत का मध्य विन्दु होता है किसी वृत में केवल एक ही केंद्र होता है.

वृत का व्यास (Diameter of Circle) :-

किसी वृत के परिधि पर के दो बिन्दुओ को मिलाने वाली वह रेखाखंड जो केंद्र से होकर गुजरती है वृत का व्यास कहलाती है .

दुसरे शब्दों में वह रेखाखण्ड जो वृत के केंद्र से होकर गुजरता है और वृत के परिधि पर दो विन्दुओ को काटता है वृत का व्यास कहलाता है . वृत का व्यास वृत की त्रिज्या की दुगनी होती है ,दिए गए वृत में रेखा AB जो की O से होकर गुजरती है वृत का व्यास है.

किसी वृत का व्यास को d द्वारा दिखाया जाता है अतः d =2r

वृत की जीवा (Chord of Circle) :-

वृत के परिधि के दो विन्दुओं को मिलाने वाली रेखाखंड को वृत की जीवा (Chord) कहा जाता है.

अथवा वह रेखाखण्ड जो वृत के परिधि को दो विन्दुओ को काटती है वृत की जीवा (Chord) कह्लाती है

ऊपर दिए गए fig में PQ वृत का जीवा है.

वृत के जीवा को बनाने वाली वृत की परिधि का अंश वृत का चाप (Chord of Circle) कहलाता है.

इसको चाप PQ लिखकर दिखाया जाता है.

वृत की त्रिज्याखंड (Sector of Circle) :-

वृत का वह भाग जो दो त्रिज्याओं और उनके संगत चाप से मिलकर बनता है त्रिज्याखंड(Sector) कहलाता है.

ऊपर दिए गये fig में OCD वृत का त्रिज्याखंड कहलता है

वृत की वृतखंड (Segment of Circle) :-

वृत की एक जीवा और उसके संगत चाप से घिरा वृतीय क्षेत्र वृतखंड (Segment) कहलाता है.

ऊपर दिए गए fig में PQ जीवा और इसके सांगत द्वारा घिरा हुआ क्षेत्र वृत का वृत खंड है जैसा की ऊपर वृत में दिखाया जाता है.

वृत की परिधि (Circumference of Circle) :-

वृत की अनुदिस चली गई दुरी वृत की परिधि(Circumference of Circle) कहलाती है.

इसको सांकेतिक रूप से C लिखा जाता है.

हम इस पोस्ट में केवल Geometry के basic चीजों के बारे में हिं चर्चा किया है इसलिए यदि आप Geometry को समझना चाहते है तो ऊपर दिए गए परिभासा को हमेसा अपने दिमाग में याद रखें.

दोस्तों finally मै आसा करता हु की Geometry के Basic Concept आपको समझ में आ गया होगा .यदि इस पोस्ट में आपको कोई doubt हो या कुछ न समझ में आया हो तो हमें कमेंट के जरिये बताये यदि आपको हमारा यह पोस्ट पसंद आया हो तो इसे like करे share करे-

यदि आप student है तो आपको निचे दिए गए पोस्ट जरुर पड़ना चाहिए-

दोस्तों ,हमारे साथ बने रहने के लिए हमें Facebook ,google + ,और Twitter पर फॉलो कीजिये