polynomial function पर आधारित basic अनुप्रयोग
नमस्कार दोस्तों , आज हम polynomial function पर आधारित basic अनुप्रयोगों को समझेंगें इसके लिए हमें polynomial function पर आधारित कुछ basics terms को जानना बहुत जरुरी है तो आइये इसे हम समझने की कोसिस करते हैं.
polynomial function( बहुपद ) क्या है –
Polynomial Function(बहुपद) वैसे बिजिय ब्यंजको को कहा जाता है जिसके चरों का power (घात) एक धनात्मक पूर्णाक (Positive Integer) हो.
अथवा ,दुसरे शब्दों में हम कह सकते है की वैसे बिजिय व्यंजक जो निम्न लिखित दिए गये फॉर्म में होते है polynomial function कहलाते है –
P(X) =A1Xn +A2Xn-1 +A3Xn-2 +A4Xn-3 +A5Xn-4 +A6Xn-5 + ………………+AM Xn-m-1
ऊपर दिए गए समीकरण में n एक धनात्मक पूर्णाक (Positive Integer) है जहाँ , n>m है. इसे हम निचे दिए गए समीकरणों से समझेगें.
जैसे- x+3 ,x-4 ,2x+1 ,3x-2 , 2x+8 ,3x2 +8x +9 , इत्यादि polynomial के उदहारण है ,ये सारे x चर के बहूपद है.इनको हम बिजिय ब्यंजक भी कहते है
लेकिन सारे बहुपद बिजिय ब्यंजक हो सकते है लेकिन सारे बिजिय ब्यंजक बहुपद नहीं हो सकते .इसको हम आगे दिए गए उदाहरण के साथ समझेगें.
X2 +5X +3 को x चर का बहुपद और y2 +8y +8 को y चर का बहुपद कहा जायेगा इसको हम Polynomial Function के रूप में निम्नलिखित तरीके से लिखेगें-
P(x)= X2 +5X +3 , को x चर का Polynomial Function कहा जायेगा .
P(y)=y2 +8y +8 , को y चर का Polynomial Function कहा जायेगा .
- वास्तविक संख्याओं से सम्बंधित अनुप्रयोगों पर आधारित प्रश्नों को हल करना सीखें
रोमन संख्या लिखने के नियम और इसपर आधारित प्रश्नों को हल करना सीखें
बीजीय ब्यंजक (Algebraic Terms ) क्या है-
चर()variables ) और अचर (Constant) राशियों को मिलाने से जो पद हमें मिलता है बिजिय ब्यंजक कहलाता है ,
जैसे -x+3 ,x-4 ,2x+1 ,3x-2 , 2x+8 ,3x2 +8x +9 , ये सारे ब्यंजक बीजीय व्यंजक के उदहारण है .अब हम चर और अचर पदों के बारे में समझाते है .
चर राशी (Variables Quantity) :-
दिए गए बीजीय ब्यंजक (Algebraic terms) के वैसे पद जिनके मान बदलते रहते है चर कहलाते है ,चर को हमेसा अंग्रेजी वर्णमाला (English Alphabet) के अक्षरों द्वारा दिखाया जाता है
उदहारण के लिए -a, b, c, p , q , r , x , y , z इत्यादि चर है.
जैसे- 3x2 +8x +9 में x चर रासी है ,इसे हम x चर का बहुपद कहेंगे.
अचर राशी(Constant Quantity) :-
किसी भी बीजीय ब्यंजक (Algebraic terms) के वैसे पद जिनके मान नहीं बदलते है अचर कहलाते है,
बीजीय ब्यंजक (Algebraic terms) में आंकिक मान (Numerical value) को हम अचर राशी कहते है ,किसी भी दिए गए बिजिय ब्यंजक में आंकिक मान एक अचर राशी होती है .
जैसे- 3x2 +8x +9 में 9 एक अचर राशी है.
Coefficient of Polynomial function (बहुपदों का गुणांक):-
किसी भी दिए गए Polynomial function में किसी भी चर राशी के साथ जिस किसी भी संख्या का गुणा किया जाता है उसे हम Coefficient of Polynomial function (बहुपदों का गुणांक) कहते है .
उदहारण के लिए polynomial function 3x2 +8x +9 में x2 का गुणांक 3 है और x का गुणांक 8 है.इस दिए गए बहुपद में 8x , आठ और x के गुणनफल से प्राप्त हुआ है .
एक पदीय , द्विपदीय और त्रिपदीय polynomial function :-
यदि किसी दिए गए Polynomial function में केवल एक ही पद हो तो उसे एक पदीय बहुपद कहते है ,यदि दो पद हो तो उसे द्विपदीय बहुपद कहते है और यदि उसमे तिन पद हो तो उसे त्रिपदीय बहुपद कहते है , इसको हम निचे दिए गए उदहारण के साथ समझेगें.
जैसे- 3x2 +8x +9 ,एक त्रिपदीय बहुपद है क्योकि इसमे 3x2 , 8x और 9 तिन पद है . ठीक ईसी प्रकार ,
x+2 एक द्विपदीय बहुपद है क्योकि इसमे दो पद x और 2 है. वैसे ही 5x एक पदीय बहुपद है .
एक पदीय बहुपद के उदहारण – 2x , 5x , 6x3 etc
द्विपदीय वहुपद के उदहारण – 2x+5 ,9x+4 , 4x +6 etc
त्रिपदीय बहुपद के उदहारण -2x2 +5x + 6 ,4x2 +8x + 9 ,3x2 +7x +9 etc
संख्या रेखा पर बिजिय ब्यंजक का निरूपण :-
माना की किसी दिए गए बिजिय ब्यंजक x +5 की चर्चा करते है ,मना की संख्या रेखा पर x की स्थिति X है और x से पांच इकाई की दुरी चलने पर हमें P मिलता है इसलिए p को X+5 से निरुपित किया जायेगा.
सामान और असमान पद (Equal and Unequal Terms) वाले polynomial function :-
सामान पद वाले polynomial function :-
वैसे बिजिय ब्यंजक जिसमे चर और चर का घात सामान हो चाहे उसका गुणांक कुछ भी हो समान पद वाले विजिय व्यंजक कहलाते है , इसके कुछ उदहारण निचे दिए गए है –
- 7x ,14x ,-13x , में तीनों पदों में x है ,इसलिए यह सामान पदों वाली बहुपद है .
- 5x2 ,-9x2 , में दोनों पदों में x2 का टर्म है इसलिए यह समान पदों वाली polynomial function है
- 7xy .-5xy , में दोनों पदों में xy टर्म है अतः चर समान है ,इसलिए यह सामान पदों वाली बहुपद है .
असामान पद वाले polynomial function :-
वैसे बिजिय ब्यंजक जिसमे चर और चर का घात सामान न हो चाहे उसका गुणांक कुछ भी हो असमान पद वाले विजिय व्यंजक कहलाते है , इसके कुछ उदहारण निचे दिए गए है –
- 7x2 ,14x ,-13x3 , में पहले पद में x2 ,दुसरे पद में x है और तीसरे में x 3 है ,इसलिए यह असामान पदों वाली बहुपद है .
- 5x2 ,-9x , में दोनों पदों में अलग -अलग पद x2 ,x का टर्म है इसलिए यह असमान पदों वाली polynomial function है
- 7xy .-5xy 2 , में दोनों पदों में अलग -अलग xy ,और xy2 टर्म है अतः चर समान नहीं है इसलिए यह असमान पदों वाली बहुपद है .
बहुपद का घात (power of polynomial function):-
किसी भी बहुपद का घात उस बहुपद का सबसे बड़ा घात को कहते है ,उदहारण से इसे हम समझाने का पर्यास करते है –
- x5 -x 4 +3 , इस बहुपद में चर x का अधिकतम घात 5 है अतः बहुपद का घात 5 होगा .
- 2-y2 -y3 + 2 y8 ,इस बहुपद में चर y का अधिकतम घात 8 है इसलिए इस बहुपद का घात 8 होगा .
- 2 =2x0 ,में इस बहुपद में चर x का घात 0 होगा इस लिए बहुपद का घात 0 होगा .(x 0=1 होता है )
- 5x3+4x2+7x ,में x का अधिकतम घात 3 है इस लिए बहुपद का घात 3 होगा .
- 4-y2 ,में चर y का घात 2 है इसलिए बहुपद का घात 2 होगा .
घात के अधर पर बहुपदों के प्रकार :-
घात के आधार पर बहुपदो के निम्नलिखित प्रकार होते है.
सुन्यक बहुपद(Zero Polynomial) :-
वैसे बहुपद जिनका घात सुन्य होता है उसे सुन्यक बहुपद कहते है ,कोइ भी अचर रासी एक सुन्यक बहुपद होता है ,
जैसे -2,3,4,5, इत्यादि एक सुन्यक बहुपद के उदहारण है
रैखिक बहुपद( Linear polynomial):-
वैसे बहुपद जिसका घात एक हो उसे हम रैखिक बहुपद कहते है ,रैखिक बहुपद में x का अधिकतम घात 1 होता है.
जैसे – 2x+5 , 9x-8 , 7 x+4 इत्यादि रैखिक बहुपद के उदहारण है .
द्विघातीय बहुपद (quadratic polynomial) :-
वैसे बहुपद जिसका घात 2 होता है वैसे बहुपद को हम द्विघातीय बहुपद कहते है .द्विघातीय बहुपद में x का अधिकतम घात 2 होता है .
जैसे -x2 +2x +3 , 2x2 + 8x – 9 द्विघातीय बहुपद है ,क्योकि इसका अधिकतम घात 2 है .
त्रिघातीय बहुपद (qubic polynomial ):-
वैसे बहुपद जिसका घात 3 हो उसे हम त्रिघातीय बहुपद कहते है ,त्रिघातीय बहुपद में x का घात 3 होता है .
जैसे – x 3 +2x2 +3x +5 , एक त्रिघातीय बहुपद का उदहारण है क्योकि इसमे x का अधिकतम घात 3 है .
Note:-किसी बहुपद में बहुपद का अधिकतम घात जितना होता है ,बहुपद को उतने ही घात का बहुपद कहा जाता है.
बहुपद को पहचाने का सबसे आसान तरीका :-
यदि कोइ बिजिय ब्यंजक के सभी पदों का घात एक धनात्मक पूर्णाक हो तो वह बिजिय ब्यंजक बहुपद होता है
यदि कीसी बिजिय ब्यंजक का किसी पद का घात कोई भिन्न (fraction) हो या कोई ऋणात्मक पूर्णाक (Negative Integer) हो तो वह बिजिय व्यंजक बहुपद नहीं होगा. इसे हम निचे दिए गए उदहारण के साथ समझते है
- 4x2 -3x +7 ,एक बहुपद है क्योकि चर x के घात एक 2,और 1 है जो की positive integer है .
- y 2 +√2 ,एक बहुपद है ,क्योकि y का अधिकतम घात 2 है .
- 3√t +t√2 = 3t1/2 +t√2 ,एक बहुपद नहीं है क्योकि यहाँ चर रासी का घात 1/2 है .
- y +2/y =y+2y -1 , यह एक बहुपद नहीं है क्योकि y पर घात -1 है जो एक negative number है.
बिजिय व्यंजको का जोड़ और घटाव :-
दोस्तों बिजिय व्यंजको में जोड़ और घटाव केवल समान पदों में ही किया जाता है ,बिजगणित में दो असमान पदों के बिच में जोड़ और घटाव संभव नहीं है ,तो निचे बिजिय ब्यंजको को जोड़ने और घटने के बिसय में हम अध्यन करते है –
बिजिय ब्यंजको का जोड़ :-
जब बिजिय ब्यंजको को आपस में जोड़ा जाता है तो तो हम योगफल केवल सामान पदों में ज्ञात करते है ,और असमान पदों को हम जैसे के तैसे लिख देते है ,इसे हम उदहारण के तौर पर निचे दिए गए नियमों और उदहारण से समझाने के कोसिस करते है –
- हमेसा सामान चरों(एक ही जाती के चर ) वाले पदों को हिं आपस में जोड़ा जाता है जैसे ,2x को 3x2 में नहीं जोड़ा जा सकता है क्योकि x और x 2 दोनों अलग अलग चर है ,लेकिन x2 और 5x2 को आपस में जोड़ देंगे और यह 6x2 हो जायेगा.
- यदि एक ही जाती का चर हो और एक ही जाती का चिन्ह हो तो हम ब्यंजको को आपस में जोड़ देते है जैसे यदि x2 और 2x2 हो तो हम आपस में जोड़ देते है
- और एक ही जाती का चर हो और दो जाती का चिन्ह हो तो हम इसे आपस में घटा देते है .जैसे 2x2 और -x2 है तो दोनों को घटा दिया जाता है.
- लेकिन यदि दो से अधिक पद हो तो सामान चिन्ह वाले पदों को आपस में जोड़ दिया जाता है और फिर यदि दो अलग अलग चिन्ह के पद है तो जिस पद का वैल्यू अधिक हो उसमे से कम वैल्यू वाले पद को घटा दिया जाता है ,और जिसमे से घटाया जाता है उसी का चिन्ह लिखा जाता है ,उदहारण के लिया 2x, -8x ,6x ,-7x इन चार पदों को जोड़ना है तो (2x +6x)+(-8x-7x) =8x-15x =-7x ans
- हमेसा बिजिय ब्यंजको को जोड़ने के लिए किसी पद को हमेसा सामान पदों के निचे ही लिखा जाता है जैसा की निचे दिखाया गया है
जैसे –
दूसरी विधि-
1 Q. बिजिय व्यंजक x +2 , 6x+8 ,और 5x2 +9x +8 का योगफल ज्ञात करें .
हल :- (x+2 )+(6x+8) +(5x 2 +9x +8)
=5x 2 + (9x+6x +x)+(2+8+8)
=5x2 +16x +18 ans
2 Q. बिजिय व्यंजक 7x2 -4x+5 , 2x2 +8x-6 और -3x2 +6x+7 का योगफल ज्ञात करें .
हल :- (7x2 -4x+5) + (2x2 +8x-6 ) + (-3x2 +6x+7 )
= (7x 2 +2 x2 – 3x2 ) +(-4x +8x+6x) +(+5-6+7)
=6x2 +10x +6 ans
3 Q. बिजिय ब्यंजक 7xy +5yz -3xz , 4yz + 9zx -4y और -3xz +5x -2xy का योगफल ज्ञात करें .
हल :- (7xy +5yz -3xz ) + (4yz + 9zx -4y) + ( -3xz +5x -2xy )
=7 xy +(5yz+4yz )+(3xz+9xz -3xz) -4y +5x -2xy
=7xy +9yz+3zx-4y+5x -2xy Ans
बिजिय ब्यंजको का घटाव :-
जब बिजिय ब्यंजको को आपस में घटाया जाता जाता है तो तो हम घटाव केवल सामान पदों में ज्ञात करते है ,और असमान पदों को हम जैसे के तैसे लिख देते है इसे हम उदहारण के तौर पर निचे दिए गए नियमों और उदहारण से समझाने के कोसिस करते है
- हमेसा सामान चरों(एक ही जाती के चर ) वाले पदों को हिं आपस में घटाया जाता है जैसे ,2x को 3x2 में नहीं घटाया जा सकता है क्योकि x और x 2 दोनों अलग अलग चर है ,लेकिन x2 को 5x2 में घटा देंगे और यह 4x2 हो जायेगा.
- एक ही जाती का चर हो और एक ही जाती का चिन्ह हो तो हम ब्यंजको को आपस में जोड़ देते है जैसे यदि x2 और 2x2 हो तो हम आपस में जोड़ देते है
- और एक ही जाती का चर हो और दो जाती का चिन्ह हो तो हम इसे आपस में घटा देते है .जैसे 2x2 और -x2 है तो दोनों को घटा दिया जाता है.
- जिस बिजिय ब्यंजक को घटाया जाता है उसका चिन्ह बदल दिया जाता है और फिर योगफल वाला प्रक्रिया दोहराया जाता है.
- यदि दो से अधिक पद हो तो सामान चिन्ह वाले पदों को आपस में जोड़ दिया जाता है और फिर यदि दो अलग अलग चिन्ह के पद है तो जिस पद का वैल्यू अधिक हो उसमे से कम वैल्यू वाले पद को घटा दिया जाता है ,और जिसमे से घटाया जाता है उसी का चिन्ह लिखा जाता है ,उदहारण के लिया 2x -8y में से 6x -7y को घटाना है तो (2x -8y ) – (6x -7y) =2x-8y-6x+7y=-4x-y ans
- हमेसा बिजिय ब्यंजको को जोड़ने के लिए किसी पद को हमेसा सामान पदों के निचे ही लिखा जाता है जैसा की निचे दिखाया गया है
- जिस बिजिय ब्यंजक में से घटाया जाता है.हमेसा उसी का चिन्ह लिखा जाता है.
- किसी भी बिजिय ब्यंजक में किसी भी पद का चिन्ह उस पद के बाइ ओरहोता है जैसे 2x-3y+4z में 2x का चिन्ह + है और 3y का चिन्ह – है और 4z का चिन्ह + है ,जिस पद के पहले कोइ चिन्ह नहीं रहता है उस पद का चिंन्ह + माना जाता है .
जैसे:-
दूसरी विधि :-
जैसे- 1 Q. बिजिय व्यंजक 7x2 -4xy +8y2 +5x -3y में से 5x 2 -4y2 +6y -3 को घटाइए.
हल :- (7x2 -4xy +8y2 +5x -3y ) – (5x 2 – 4y2 +6y -3)
व्यंजक (5x 2 4y2 +6y -3) के पहले – का चिन्ह है इसलिए इसके व्यंजको का चिन्ह बदल जायेगा –
=7x2 -4xy +8y2 +5x -3y – 5x 2 + 4y2 -6y +3
=(7x2 – 5x 2 ) +(8y2 +4y2) +(-4xy ) +5x +(-3y-6y) +3
=2x 2 +12y 2 -4xy+5x-9y +3 Ans
2 Q. बिजिय व्यंजक 4x3 + 8x 2 + 5x+ 7 में से 9x 3+ 5x 2 -6x -3 को घटाइए.
हल :- (4x3 + 8x 2 + 5x+ 7 ) – (9x 3+ 5x 2 -6x -3 )
=4x3 + 8x 2 + 5x+ 7 -9x 3 – 5x 2 + 6x +3
=-5x3 +3x2 +11x+ 10 Ans
अणुभार और अणुसूत्र निकालना सीखे(Basic Chemistry)-10th और (10+2)th साइंस student जरुर पढ़े
संख्याओं की प्रकार और विभाज्यता के नियम आपके कम्पटीशन परीक्षा में जरूर पूछे जायेंग
बिजिय ब्यंजको का गुणनफल और भागफल :-
बिजिय ब्यंजको का गुणनफल :-
दोस्तों बिजिय ब्यंजको का गुणनफल ठीक अंक गणितीय गुणनफल जैसा है इसके कुछ सामान्य नियम है जो निचे दिए गए है सबसे पहले हम इसे हम समझने का प्रयास करते है –
- जब हमें दो बिजिय ब्यंजको का आपस में गुणनफल ज्ञात करना होता है तो पहले बिजिय ब्यंजक के पत्येक टर्म का दुसरे बिजिय ब्यंजक के प्रत्येक टर्म से उसके चिन्ह के साथ गुणनफल ज्ञात करते है .
- इस प्रक्रिया में चिन्हों के गुणनफल का विसेस ध्यान रखा जाता है जैसे – (+)X(+)=+ , (-)X(-)=+ , (+)X(-)=- , (-)X(+)=- .
- इसके बाद जो भी हमें मिलता है उसे आपस में योगफल ज्ञात कर लेते है .
- प्राप्त विजिय ब्यंजक दिए गए बिजिय ब्यंजको का गुणनफल होता है .
जैसे :- इस नियम को निचे दिए गए उदाहर्नो के साथ समझते है –
- 4 * x =4x
- x * 3y =3*x*y =3xy
- 5x*3y =5*x*3*y=15xy
- 5x*(-3y) =5*x*(-3)*y =-15xy
- 2x*5y*7z =2*x*5*y*7*z=70xyz
- 4xy*5x 2y2 *6x 3y 3 = 4*x*y*5*x*x*y*y*6*x*x*x*y*y*y = 120x6y6
- 3x*(5y+2 )=3x*5y+3x*2= 15xy +6x
- – 3x*(-5y+2) =(-3x)*(-5y)+(-3x*2)= 15xy-6x
- 5xy(y 2 +3) =5xy*y 2 +5xy *3 = 10xy3 +15xy
- 2x*(3x+5y)=6x2 + 10xy
- x2 *(2xy – 5z ) =x*x*2*x*y – 5*x*x*z =2x3y – 5x2z
- 3x*(4x 2 +5x+7)=3x*4x*x +3x*5x +3x*7 =12x3 + 15x2 +21x
- (3x+4y)*(2x+3y) =3x(2x+3y)+4y(2x+3y)=6x 2 +9xy +8xy+12y2 =6x2 +17xy +12y2
Note :- ऊपर दिया गया “*” का चिन्ह गुणनफल का Symbol है


बिजिय ब्यंजको के गुणनफल के कुछ खास उदहारण :-
निम्न लिखित दिए गए बिजिय ब्यंजको का गुणनफल ज्ञात करें –
1 Q. (x-4)*(2x+3)
हल :-(x-4)*(2x+3) = x(2x+3)-4(2x+3)
=2x2 +3x-8x-12 = 2x2 -5x -12 Ans
2 Q. (x-y)*(3x+5y)
हल :-(x-y)*(3x+5y) =x(3x+5y)-y(3x+5y)
=3x2 +5xy – 3xy -5y2 = 3x2 +2xy -5y2 Ans
3 Q.(x+7)*(y-5)
हल :- x(y-5)+7(y-5)=xy-5x +7y-35 Ans
4 Q. (x 2 +2y2 )*(5x-3y)
हल:- x 2 *(5x-3y)+2y2 *(5x-3y)
=5x3 -3x2y +10xy2 -6y3 Ans
5 Q.(x+y)(2x+3y+z)-(2x-3y)*z को सरल कीजिये.
हल :– (x+y)(2x+3y+z)-(2x-3y)*z
=x(2x+3y+z)+y(2x +3y+z)-z*(2x-3y)
=2x2 +3xy+xz+2xy+3y2+yz -2zx+3yz
= 2x2 +3y2 +5xy +4xz +3yz Ans
बिजिय व्यंजको का भागफल:-
बिजिय ब्यंजको का भागफल ज्ञात करने के लिए कुछ नियमो का जान लेते है जो निचे दिए गए है
भागफल का प्रमेय :- भाज्य = (भाजक * भागफल ) +शेसफल
- सबसे पहले भाज्य और भाजक को मानक रूप में लिखते है अर्थात अवरोही (घटते हुए क्रम )क्रम में लिखते है.
- हम भाज्य के पहले पद को भाजक के पहले पद से भाग देते है जो प्राप्त होता है वह भागफल का पहला पद होता है .
- अब हम भाजक को भागफल के पहले पद से गुना करते है इस गुनफल को भाज्य से घटा देते है ,और सेसफल प्राप्त करते है .इस सेसफल को नया भाज्य मान लेते है और भाजक वाही बना रहता है
- ऊपर दिए गए नियम को फिर से दोहराते है .
- हमें भागफल का दूसरा पद प्राप्त होता है ,अब भाजक को भागफल के दुसरे पद से गुणा करते है इस गुणनफल को हम भाज्य से घटाते है.यह प्रक्रम हम तब तक दोहराते है जब तक की नए भाज्य की घात दिए गए भाजक की घात से कम न हो जाय.
- इस चरण में भाज्य सेसफल हो जाता है और भागफलों के योगफल से हमें पूर्ण भागफल प्राप्त होता है .
ऊपर दिए गए नियमों को निचे दिए गए उदहारण के साथ समझते है.
1Q. p(x) को g(x) से भाग दीजिये जहाँ पर p(x)=x +3 x 2 +1 है और g (x)= 1 +x है .
हल :- अब हम इस भाग देने की प्रक्रिया को निचे दिए गए चरणों में पूरा करेंगे
यहाँ पर p(x)=x +3 x 2 +1 भाज्य है और g (x)= 1 +x भाजक है
पहला चरण :-अब सबसे पहले हम भाज्य और भाजक को मानक रूप अर्थात इनके घातों के घटते हुए क्रमों में लिखते है
अतः भाज्य : p(x)=3 x 2 +x +1 ,भाजक : g (x)= x +1
दूसरा चरण :- अब हम भाज्य के पहले पद को भाजक के पहले पद से भाग देते है ,अर्थात 3 x 2 को x से भाग दे ते है तो हमें 3x प्राप्त होता है ,यह 3x हमारे भागफल का पहला पद होगा , 3 x 2 /x =3x =भागफल का पहला पद .
तीसरा चरण :- अब हम भाजक को भागफल के पहले पद से गुणा करते है और गुणनफल को भाज्य से घटा देते है ,अर्थात हम x+1 को 3x से गुणा करते है और
गुणनफल 3x2 +3x को भाज्य 3 x2 +x -1 से घटाते है.और सेसफल -2x-1 प्राप्त होता है .
चौथा चरण:-अब सेसफल -2x-1 को नया भाज्य मान लेते है और भाजक वाही बना रहता है अब चरण दो को पुनः दोहराने पर हमें भागफल का अगला पद प्राप्त होता है अर्थात भाज्य के पहले पद -2x भाजक के पहले पद x से भाग देने पर हमें भागफल का दूसरा पद -2 प्राप्त होता है ,-2x/x=-2 और नया भागफल= 3x-2 .
पांचवा चरण :-अब हम भाजक को भागफल के दुसरे पद से गुणा करते है और इस गुणनफल को भाज्य में से घटाते है, अर्थात हम x +1 को -2 से गुणा करते है और गुणनफल -2x-2 को भाज्य -2x-1 में से घटाते है और सेसफल के रूप में हमें 1 प्राप्त होता है.
छठा चरण :- यह प्रक्रिया तब तक दोहरायेगें जब तक की नए भाज्य की घात भाजक की घात से कम नहीं हो जाता ,इस चरण पर भाज्य सेसफल हो जाता है .और भाग्फालों के योग से हमें पूर्ण भागफल प्राप्त होता है इसप्रकार –
भागफल = ३x-2 और सेसफल =1 ,इसे हम निचे दिए प्रक्रिया द्वारा समझते है -
2 Q.बिजिय ब्यंजक x3 +1 को x +1 से भाग देने पर प्राप्त भागफल और सेसफल ज्ञात कीजिये.
हल:-
दोस्तों ,हमारे साथ बने रहने के लिए हमें Facebook ,google + ,और Twitter पर फॉलो कीजिये






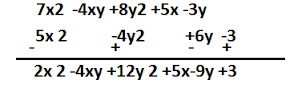


















0 टिप्पणियाँ
Please Don't enter any spam link into the comment box