संख्याओं की प्रकार और विभाज्यता के नियम

हेल्लो दोस्तों आज हम संख्याओं की प्रकार और विभाज्यता के नियम के बारे में बिसेस चर्चा करेगें

सबसे पहले संख्याये मुख्यतः कितने प्रकार के होते है समझने का प्रयास करते है.

संख्याओं की प्रकार (Types of Numbers ):-

संक्यायें(Numbers) मुख्यतः 11 प्रकार की होती है ,इनके बारे में निचे डिटेल में दिया गया है

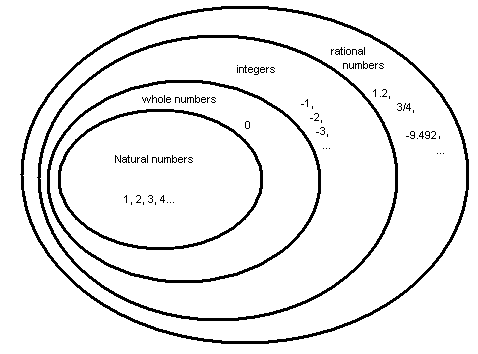
(1)प्राकृतिक संक्या (Natural Number):-

वैसी संख्या जिनका प्रयोग चीजों को गिनने के लिए किया जाता है ,प्राकृतिक संख्यायें कहलाती है

अथवा वैसी संख्या जो 1 से सुरु होती है प्राकृतिक संख्या कहलाती है

Ex:- 1 , 2 , 4 , 5 , 6 , 7 , 8 , 9 , 10 …….ये सब प्रकृतिक संखयों के उदहारण हैं |

(2)पूर्ण संख्या (Whole Number ):-

वैसी संख्याएं जो 0 से सुरु होती अहि और अनंत तक जाती है ,पूर्ण संख्याए कहलाती है

Ex :-0, 1, 2, 3, 4, 5, 6 , …….. यह पूर्ण संख्याओं के उदहारण है , प्रत्येक प्राकृतिक संख्या एक पूर्ण संख्या होती है ,लेकिन प्रत्येक पूर्ण संख्या एक प्राकृतिक संख्या नहीं होती ,0 प्राकृतिक संख्या नहीं है , यह एक पूर्ण संख्या हैं |

(3)धनात्मक संख्या (positive numbers ):-

वैसी संख्या जिनकी चिन्ह धनात्मक हो उसे धनात्मक संख्या कहते हैं ,धनात्मक संख्याओ के पहले किसी भी चिन्ह का प्रयोग नहीं होता |

Ex :- 1,2,3,4,5,6,,7………,2.3,4.5…..etc धनात्मक संख्याओ के उदहारण है

(4) ऋणात्मक संख्या (Negative Number ):-

वैसी संख्याए जिसका चिन्ह ऋणात्मक हो ऋणात्मक संख्याए कहलाती है ,ऋणात्मक संख्याओ के पहले हमेसा ऋण “-” का चिन्ह लगा होता है

Ex:–2, -4 ,-6 , -12 ,-14 ,….. इत्यादि ऋणात्मक संख्याओ के उदहारण है

(5) पूर्णांक (Integers ):-

वैसी संख्यओं का समूह जो धनात्मक या ऋणात्मक हो पूर्णांक संख्याए कहलाती है ,0 एक धनात्मक पूर्णांक है, पूर्णांक मुख्यतः धनात्मक या ऋणात्मक होते है ,दशमलव सख्याये पूर्णांक के श्रेणी में नहीं आते |

Ex. ….-3, -2 ,-1 ,0,1,2,3 ….. इत्यादि संख्याये पूर्णांक संख्याओ के उदहारण है

धनात्मक पूर्णाकों का समूह = {1,2,3,4,5,6,7,…..} ये सारे धनात्मक पूर्णाकों के समूह है

ऋणात्मक पूर्णांको का समूह ={-1 ,-2 ,-3, -4 ,-5,-6 } ये ऋणात्मक पुर्णाकों के समूह है

(6)सम संख्या (Even Numbers ):-

वैसी संख्याए जिनमे 2 से पूरा -पूरा भाग लग जाये अथवा,2 से विभाजित हो , सम संख्याए कहलाती है

Ex -2,4,6,8,10, …….ये सम संख्याओ के उदहारण है

(7)विसम संख्या (Even Number ):–

वैसी संख्याए जिसमे 2 से पुरा -पूरा भाग न लगे ,अथवा वैसे संख्याए जो 2 से विभाजित नहीं होती है ,विसम संख्याए कहलाती है –

Ex- 1 ,3 ,5 ,7, 9,13 ,15 ,………….etc विसम सख्याओ के उदहारण है

(8)परिमेय संख्या (Rational Number):-

वैसी संख्याए जो p/q के रूप में हो लेकिन q ,सुन्य के बराबर न हो ,परिमेय संख्याए कहलाती है

Ex- 2/3,4/5 ,6/7 .9/2 इत्यादि परिमेय संख्याओ के उदहारण है ,परिमेय संख्याए धनात्मक भी हो सकती है ,और ऋणात्मक भी , -2/3,-4/5 ऋणात्मक परिमेय संख्या है ,और +1/2,3/4,6/7 धनात्मक परिमेय संख्या है

(9)अपरिमेय संख्या (Irrational Number) :-

वैसी संख्या जिसको पूर्णतः p/q के रूप में नहीं लिखा जा सकता अपरिमेय संख्या कहलाता है. उदहारण :-root 5,root 6, root 7 ,etc अपरिमेय संख्याओ के उदहारण है

(10)अभाज्य संख्या (Prime Number):-

वैसी संख्याये जो 1 से या स्वयं से विभाजित होती है ,अपरिमेय संख्या कहलाती है

Ex. 3 ,5 ,7 ,13 ,17 ,etc अपरिमेय संख्याओ के उदहारण है

(11)भाज्य संख्या (Composite Number ):–

वैसी संख्या जो 1 और स्वयं के आलावा भी किसी संख्या से विभाजित होती है ,भाज्य संख्या कहलाती है . उदहारण- 12,21,34 ,56 ,ये भाज्य संख्या के उदहारण है .

(12)वास्तविक संख्या (Real Number ):-

वैसी संख्यए जिसका वर्ग हमेसा सुन्य या सुन्य से बड़ा हो वास्तविक संख्याये कहलाती है ,अतः माना की ,X कोई Real Number है ,तो X*X >=0 , Ex. 3, 2.5 , 4.6 ,7, root 8 ये सारे वास्तविक संख्याओ के उदहारण है ,

ऊपर दिए गए सारे संख्याओ के प्रकार वास्तविक संख्याओ के उदाहराण है.

विभाज्यता के नियम (Rule of Divisibility):-

कोई संख्या किस किस संख्या से विभाजित है ,पता करने के लिए कुछ निश्चित नियम बनाये गए है जिसे हम विभाज्यता के नियम कहते है

(1)1 से विभाज्यता:-

1 से सभी संख्याये विभाजित होती है , उदाहराण- 1,2,5, 9,13 ,23 ,etc

(2)2 से विभाज्यता के नियम :-

वैसी संख्यायें जिनके इकाई के स्थान पर 0, 2, 4, 6, 8 हो 2 से पुर्णतः विभाजित होती है ,

उदहारण – 22 ,12 ,18,98 ,122 ये सभी संख्याए 2 से विभाज्य होगें

(3) 3 से विभाज्यता के नियम :-

कोई भी संख्या 3 से विभाजित होती है यदि उस संख्या के सरे अंको का योग 3 से बिभाजित होगी .

उदहारण :- (i).231 =2+3+1 =6 ,यह संख्या 3 से विभाजित है अतः 231 भी 3 से विभाजित होगी.

(ii)695421 =6+9+5+4+2+1=27 ,3 से विभाजित है अतः दी गई संख्या भी 3 से विभाजित होगी

(4) 4 से विभाज्यता के नियम :-

कोई भी संख्या 4 से विभाजित होगी ,यदि दी गई संख्या के अंतिम दो अंक 4 से विभाजित होगी.

उदाहराण -(i) 6879376 ,यहाँ 76 , 4 से विभजित है अतः दी गई संख्या 4 से विभाजित होगा

(ii) 496138 ,यहाँ 38 ,4 से विभाजित नहीं होगी ,अतः दी गई संख्या 4 से विभाजित नहीं होगी

(5) 5 से विभाज्यता के नियम :-

कोई भी संख्या 5 से विभाजित होगी यदि उस संख्या के इकाई के अंक पर 0,या 5 हो .

उदहारण- 7849320 ,76895 ,68790, ये सभी संख्याओ के इकाई के स्थान पर 0,5 है अतः ये 5 से विभाजित होगी

(6)6 से विभाज्यता के नियम :-

वो सभी संख्याये 6 से विभाजित होगी ,यदि वो 2,और 3 से विभाजित होतो है .

उदाहराण-222 ,ये संख्या 6 से विभाजित होगी क्योकि यह 2 से भी विभाजित है और 3 से भी विभाजित है

(7) 7 से विभाज्यता का नियम: –

यदि किसी संख्या के इकाई के अंक का दोगुना बाकी अंकों से बनी संख्या से घटाने पर प्राप्त संख्या 7 से विभाजित होती है तो वह संख्या भी 7 से पूर्णत: विभाजित होगी।जैसे -2170, 6377 ,348 आदि ।

उदाहराण :-(i)जाँच-348 =34 -8*2 =34-16 =18 ,7 से विभाजित नहीं है ,अतः दी गई संख्या 7 से विभाजित नहीं होगी

(ii)6377=637 – 14=623 =62-3*2=62-6=56 ,7 से विभाजित है ,अतः दी गुई संख्या भी 7 से विभाजित होगी

Note-यदि दी गई संख्या बड़ी हो तो , यह प्रक्रिया दोहराया जायेगा.

(8)8 से विभाज्यता का नियम :-

यदि किसी संख्या के इकाई, दहाई और सैकड़े के अंकों से बनी संख्या 8 से विभाजित होती है अथवा किसी सख्या के अंतिम तीन अंक 8 से विभाजित होती है तो वह संख्या भी 8 से विभाजित होती है। जैसे -4528, 69456, 1000 आदि

उदाहराण- (i)4528 ,इसमे अंतिम तीन अंक 528, 8 से विभाजित होती है अतः दी गई संख्या 8 से विभाजित होगी.

(ii)69456 ,इसमे 456 ,8 से विभाजित है अतः दी गई संख्या भी 8 से विभाजित होगी

(9)9 से विभाज्यता का नियम :-

जिस संख्या के अंकों का योग 9 से विभाजित हो जाता है, तो वह संख्या भी 9 से विभाजित होती है। जैसे – 4536, 7839, 12348 आदि।

उदाहराण:- जाँच-4536 =4+5+3+6=18 ,9 से विभाजित है ,अतः दी गई संख्या भी 9 से विभाजित होगी

78363=7+8+3+6+3=27, 9 से विभाजित है ,अतः दी गई संख्या भी ,9 से विभाजित होगी

(10)10 से विभाज्यता का नियम :-

जिस संख्या के इकाई के स्थान पर 0 आता है, तो वह संख्या 10 से विभाजित होती है।

जैसे- 680, 450 , 10000, 78640 आदि।

(11)11 से विभाज्यता का नियम :-

यदि किसी संख्या के सम स्थानों पर आए अंकों के योग और विषम स्थानों पर आए अंकों के योग का अंतर 0 हो या 11 से विभाजित होता हो तो वह संख्या भी 11 से विभाजित होगी।

जैसे -2442, 9482 आदि , जाँच:-2442 =(4+2)-(4+2)=0 , अतः दी गई संख्या 11 से विभाजित है

9482=(9+8)-(4+2)=11 ,11 से विभाजित होगी ,अतः दी गई संख्या भी 11 से विभाजित होगी .

(12)12 से विभाज्यता का नियम :-

जो संख्या 3 और 4 दोनों से विभाजित होती है वह संख्या 12 से भी विभाजित होती है।

जैसे – 6300 , 21408 आदि ,दी गई संख्या 3 और 4 दोनों से विभाजित होगी ,इसके लिए हम अलग – अलग दोनों स्संख्याओ से divisibility(विभाज्यता ) को चेक करेगें

(13)13 से विभाज्यता का नियम :-

किसी संख्या के इकाई के अंक का चार गुना बाकी अंकों से बनी संख्या में जोड़ने पर प्राप्त योगफल यदि 13 से विभाजित होता है तो वह संख्या भी 13 से विभाजित हो जाएगी। जैसे – 2579

जाँच -2579 =257 +9*4 =257+36 = 293 ,13 से विभाजित नहीं है अतः दी गई संख्या भी 13 से विभाजित नहीं होगी.

(14) 14 से विभाज्यता का नियम :-

यदि कोई संख्या 7 और 2 से विभाजित है तो वह संख्या 14 से भी विभाजित होगी .

उदहारण- 136 ,294 , ये संख्यांये 7 और 2 दोनों से ही विभाजित है ,इसकि हम विभाज्यता बारी -बारी से चेक करेंगे

(15)15 से विभाज्यता का नियम :-

जो संख्या 3 और 5 दोनों से विभाजित होती है वह संख्या 15 से भी विभाजित होती है।

जैसे – 6300 , 21240, 43125 आदि ,दी हुई संख्या 3 और 5 दोनों से ही विभाजित है ,अतः यह 15 से भी विभाजित होगी

(16)16 से विभाज्यता का नियम :-

कोई भी दी गई संख्या 16 से विभाजित होगी ,यदि इस संख्या के अंतिम 4 अंक 16 से विभाजित होगा

उदाहराण:-1236 etc,यह संख्या 16 से विभाजित है

प्रतियोगी परीक्षा आधारित अन्य महत्वपूर्ण विभाज्यता संबंधी नियम :-

निचे दिए गए प्रमेयो में n एक प्राकृतिक संख्या है.

n3 – n सदैव 6 से विभाजित होगा. जाँच- माना की n एक प्राकृतिक संख्या है ,जहाँ (i)n = 3 , n3 – n =27 -3 =24 ,यह 6 से विभाजित है ,(ii)n =4 ,n3 – n =64 -4=60 ,यह संख्या 6 से विभाजित है
(10n-1) एक भाज्य संख्या है, यदि n एक सम संख्या है तो यह 11 से भी विभाजित होगी। ,जाँच -माना की n=2(सम संख्या) है .(10n-1)=100-1=99 , यह एक भाज्य संख्या है, यह संख्या 11 से विभाजित होती हैं.
(an+bn) सदैव (a+b) से विभाज्य होती है,यदि n एक विसम संख्या है ,जाँच-माना n=3,a3+b3=(a+b)(a2-ab+b2) ,यह सर्वसमिका (a+b )से विभाजित होती है
(an– bn) सदैव (a-b) से हमेसा विभाज्य होती है और यदि n एक सम संख्या है तो यह (a+b) से भी विभाज्य होगी. जाँच- माना की n=2(सम संख्या हो ) तो , (a2-b2) = (a+b) (a-b),यह संख्या (a+b) से विभाजित होगी ,अब n=3(विसम संख्या ) माना ,a3-b3=(a-b)(a2-ab+b2) , यह संख्या भी a-b से विभाजित होगी .

किसी भी संख्या “P” के अभाज्य होने की जाँच करना :-

माना की p कोई दी गई प्राकृतिक संख्या है और हमें जाँच करना है की p एक अभाज्य संख्या है या नहीं ,इसकी जाँच हम निचे दिए गए स्टेप्स में करेगे

P एक प्राकृतिक संख्या है ,इसके अभाज्य होने की जाच करना है .
मान लो n कोई संख्या है ,जहाँ ,n*n>=p
n से छोटा सभी अभाज्य संख्याये ज्ञात करे .
यदि n से छोटे किसी भी अभाज्य संख्या से ,p विभाजित होती है तो ,p एक अभाज्य संख्या नहीं है .
यदि n से छोटे किसी भी संख्या से p विभाजित नहीं होती है तो p एक अभाज्य संख्या है .

उदहारण-137 ,173 ,319 ,437 की अभाज्यता की जाँच करें.

(i)137 :-12*12>=137 ,12 से छोटा सभी अभाज्य संख्याए =2,3,5,7,11 ,अब उपर दिए गए नियमो से हम विभाज्यता की जाँच करेगें ,इन संख्याओ में से किसी से भी 137 विभाजित नहीं है अतः 137 एक अभाज्य संख्या है

(ii)173 :-14*14>=173 ,14 से छोटा सभी अभाज्य संख्याए =2,3,5,7,11 ,13 , अब उपर दिए गए नियमो से हम विभाज्यता की जाँच करेगें ,इन संख्याओ में से किसी से भी 173 विभाजित नहीं है अतः 173 एक अभाज्य संख्या है

(iii)319 :-18*18>=319 ,18 से छोटा सभी अभाज्य संख्याए =2,3,5,7,11 ,13,17 , अब उपर दिए गए नियमो से हम विभाज्यता की जाँच करेगें ,इन संख्याओ में से किसी से भी 319 विभाजित नहीं है अतः 319 एक अभाज्य संख्या है

(iv)437 :-21*21>=437 ,21 से छोटा सभी अभाज्य संख्याए =2,3,5,7,11 ,13 ,17,19, अब उपर दिए गए नियमो से हम विभाज्यता की जाँच करेगें ,इन संख्याओ में से किसी से भी 437 विभाजित नहीं है अतः 437 एक अभाज्य संख्या है

विभाज्यता के नियमो पर आधारित प्रश्न :-

1.यदि संख्या 517324 , 3 से पूरा – पूरा विभाजित होती है तो , के स्थान पर कौन सा संख्या होगा ?

Ans:- 5+1+7++3+2+4=(22+) ,3 से विभाजित है अतः 22 से ठीक बड़ा 3 से विभाजित संख्या 24 ,इसप्रकार * = 24-22=2

अतः दी गई संख्या में * के जगह पर 2 होगा

**2.यदी संख्या 972156 , 11 से विभाजित है तो के स्तन पर कौन सी संख्या होगी ?**

Ans :-972156 =(9+2+5+6)-(7+1+)=22-8-=14- =0या 11 से बिभाजित होगा अतः 14-11=3 ,अतः *के जगह पर3 होगा

दोस्तों मै आसा करता हु की संख्याओं की प्रकार और विभाज्यता के नियम से सम्बंधित प्रश्नों का हल करना आपको आ गया होगा ,यदि इस पोस्ट में आपको कोई doubt हो या कुछ न समझ में आया हो तो हमें कमेंट के जरिये बताये यदि आपको हमारा यह पोस्ट पसंद आया हो तो इसे like करे share करे-

यदि आप student है तो आपको निचे दिए गए पोस्ट जरुर पड़ना चाहिए-

दोस्तों ,हमारे साथ बने रहने के लिए हमें Facebook ,google + ,और Twitter पर फॉलो कीजिये

Ad Code

Ticker

संख्याओं की प्रकार और विभाज्यता के नियम आपके कम्पटीशन परीक्षा में जरूर पूछे जायेंगे